MAT 101 Mathematical Modeling Using the Computer

Predicting the Future and Other Mathematical Magic

Objectives:

Using Trendlines

www.coyleandsharpe.com/gallery/8.html

Trendlines are the mathematician's version of the crystal ball. They allow us to predict the future with some degree of accuracy, at least when it comes to numbers. Trendlines can be used to predict future expenses (for example, term bill prices), business sales, population growth, climate, or anything else that has a numeric value. This makes them a very useful tool because they can help us make decisions about the future. Luckily, Excel can calculate these automatically when we give it information from the past.

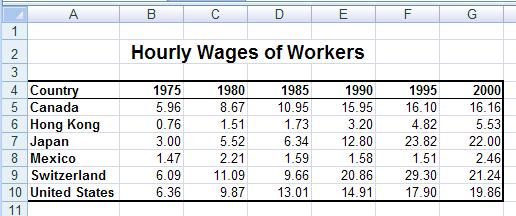Houly wagesThere are two different ways that trendlines can be generated. The easiest and best way is by utilizing the "Add Trendline" feature under Chart in the top menu bar. (This is the method outlined in the text, Matering Excel, and we will also go through it here with the data given on the right which represents how much money workers in a variety of countries make per hour.

 First of all, you need to highlight all of the data, including the labels.  (In this example, that is A3:G9.)  Then from the Insert Tab, choose theChart called XY (Scatter), and making sure Excel correctly identifies that your data is in rows or you need to push the swithch rows and columns:

    Hourly Wages

This gets us a nice graph.  To add a trendline, you right-click on a data-point and choose "Add Trendline" and follow the directions in the wizard.

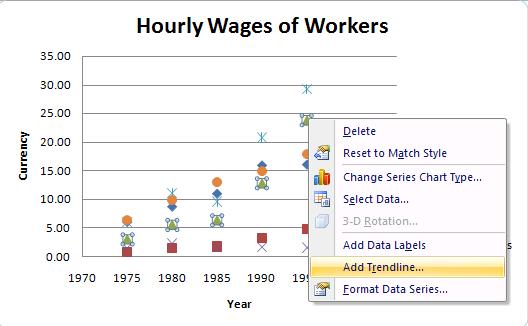
Add Trendline
 

Projections

Note that the linear equations can be used to predict the future in any year!  How well do these equations work for prediction?  That is where R-squared comes in.

R-Squared (aka R2)

R-squared (R2) is always a number between 0 and 1.  Here R is formally called the square of the coefficient of correlation and can range from -1 to 1.  R-squared is, of course, the square of R, which serves to make it non-negative. Suppose that you have ordered pairs of data (x, y) . The hope is to find a linear relationship by which the variable x can be used to predict the value of y. Of course, we don't expect this relationship to be exact, so the predictions will not be perfect, and R-squared is a measure of how "good" we expect those predictions to be. When R-squared is close to 1, the relationship is almost exactly linear and the predictions will be almost perfect. When R-squared is close to 0, the linear equation we get does a poor job of predicting y when x is given.  R-squared gives the percent of that variability that is "explained" by x.

Using Auto-Fill Instead of Trendlines

The second, less-flexible, more prone to error, and more difficult method for predicting the future utilizes the Fill function as we have already seen in class. When data is entered into Excel, we can click on the past data and then fill over (or down) to future data. Warning-- the use of this method, will  lead to errors when the data is not evenly spaced!  But, if the data is evenly spaced, autoful can also be used to give you a complete linear projection. We can use the values it predicted to estimate how much compensation workers will get in 2075 ($60.40) or any other year which is a multiple of 5.  Note that using this method, you cannot predict the future in a year that is not a multiple of 5.

If your independent variable values (as in the examples above) are all equally spaced, then you can use either method for making future predictions: trendlines OR autofill. However, if your independent variable values are NOT all equally spaced (eg. 1960, 1970, 1995, 2000), then autofill will not work, so you will have to use trendlines ot get an accurate model!

 

This assignment is to be completed individually, but you may consult with one another as long as you give appropriate credit.

This assignment will be dedicated to working more with linear models that can be found using Excel's trendline feature. Please use trendlines instead of autofull for all predictions.  All of the data is actual environmental data.. You should be able to copy and paste the data into the Excel rather than retyping it. Be sure to convert from years to "number of years after..." to avoid possible rounding errors.

  1. CO2 Emissions:
    Scientists have linked the warming trend that took off in the twentieth century to the buildup of carbon dioxide (CO2) and other heat-trapping gases. By burning fossil fuels like gasoline, fuel-oil, and natural gas, people release tons of carbon into the atmosphere each year, and the amounts released each year have been increasing. To look carefully at this trend, see CO2 Emissions and use the number of years after 1950 to create a trendline.
  2. CO2 Concentrations:
    350 ppm     is the number that leading scientists say is the safe upper limit for carbon dioxide--measured in parts per million in our atmosphere. Measurements taken in Hawaii show an 18-percent increase in atmospheric CO2 concentration levels from 1959 to 2002.  To look at the numeric trend since 1959, see CO2 Concentrations, and then create a linear trendline using only the year and the mean (average) columns. From: Dr. Pieter Tans, NOAA/ESRL (www.esrl.noaa.gov/gmd/ccgg/trends/)
  3. Global Temperatures:
    The ten warmest years in the history of the planet have occurred since 1990. To look at the trend, see Global Temperatures, and use the number of years after 1880 to create a trendline.
  4. Weather Disasters:
    Even before the disasterous hurricanes of 2005, over the last two decades, floods and other weather-related disasters were among the factors prompting millions of people to migrate.  To look at the trend, see Weather Disasters and use the number of years after 1980 and  create a trendline.

Create a graph for each of these datasets with each dataset on a separate worksheet that is appropriately entitled. Then answer the following questions for each of these four data sets.

  1. Excel: Find the linear trendline model produced for this data by the Excel trendline feature that extends to 2010, being sure to include the linear equation and the R2 on the model.
  2. Paper: Write the linear equation and the R2 on the model on your paper then use the R2 value to explain whether you believe the model fits the data well.
  3. Paper: Assuming a linear model and that current trends continue, find what your mathematical model predicts about the year 2010.
  4. Paper: Explain the real world interpretation of the slope of your mathematical model.

Save your file as yourusernameA12.

You must submit the Excel document in the dropbox by the beginning of class and turn in the paper portion at the beginning of class.

As always, all work done in Excel should be formatted so that it is readable. Assignments that are unreadable due to poor formatting (either too much or too little) will recieve a lowered grade.